
"Technicity enables the human to imagine the naturally impossible." Read More
Summary
- Human beings are the only species to develop technology.
- Language had evolved before the speciation of modern humans.
- In child development the capacity to draw develops after language has fully developed.
- Drawings are constructed from abstract geometrical forms and block-filled with colour.
- Human constructions are unnaturally simple in form.
- The identified source for information on abstract line, colour, etc. is phyletic (elemental) information immanent (inherent) in primary visual cortex.
- Prefrontal cortex has the capacity to create new possibilities from memories.
- Hypothetically, the globularisation of the brain with the advent of anatomically modern humans brought about the accidental connection of prefrontal neurones to primary sensory cortex.
- This would have provided prefrontal cortex with memory information of a different quality from sensory input, thence the technicity adaptation.
- This adaptation is a major transition in life and separates modern humans from all precursor species.
- The unnatural constructions created from this elemental information can only be maintained by a system of education.
- A corollary of the later evolution of technicity relative to language is a disconnection between the two. Technicity and language meet up only in prefrontal cortex.
- Primary education, when prefrontal cortex is making its greatest connectional growth is the phase wherein technicity and language are brought into greater congruence.
- Three modes of learning are available to modern humans:
- Mode 1: pre-modern verbal/demonstrative, which we share with Neanderthals;
- Mode 2: lithic learning, “written on a slate animated in a mind”, uses meaningful marks as external memory, the “Stone Age” basis of schooling since before writing was developed;
- Mode 3: Turing teaching, which uses the computer constructionally, and is new.
- Each mode is a transition. Consequently the characteristics and benefits of a higher mode are not researchable from within a lower one.
- There is evidence to suggest that traditional teaching methods lack conceptual clarity. In literacy and numeracy they confuse children and are unfit for purpose.
- Transition to Turing teaching is the next leap in the development of education. Begun now, a minimum of a quarter century will be required for transition.
To sum up in a short phrase: Technicity enables the human to imagine the naturally impossible.
The Technicity Thesis:
The evolutionary transition to the human occurred when phyletic information in primary sensory cortex on: line, colour, motion, pitch, etc. became available for prefrontal appreciation and creative construction. Technicity, an accidental adaptation, over generations, with education, led to technology.

Introduction
As a teacher in the primary phase of education and of children with learning difficulties, I have long been fascinated by drawing. At the beginning of my career the “how and why” of this human ability did not concern me. Later, experience with children with so-called perceptual and language disabilities, where the focus was on the effects of deficit in these areas on literacy and numeracy, caused me to seek answers from psychology. I was surprised to find that psychology has little or nothing to say about our ability to draw, given the importance of writing, although language was covered in depth. So, I just got on with the job. Electronic equipment was becoming less expensive and I looked to it for assistance. Using an early electronic calculator, I successfully taught a boy who could not count the secrets of the decimal number system. The microcomputer then appeared and I bought an early BBC model B, with which I experimented with text-to-speech synthesis; the Concept® overlay keyboard; and the “LOGO” Turtle. I came to the conclusion that “the computer” was a new educational medium that demanded change in teaching method. The results gather dust in Manchester University1 but I am a master of philosophy! The English National Curriculum arrived hot on the heels of the microcomputer, followed by National Literacy and Numeracy Strategies. These emphasised use of the computer as a delivery tool within traditional teaching method. It came to be called “information and communication technology” (which also connotes pen and paper) and ICT is now assimilated as “technology” The idea that the capabilities that Alan Turing described for his conceptual computer: to read, write and thereby do arithmetic, might alter education is actively resisted. The old headline was “Calculators rot children’s brains” and computers would “Dumb down” school. My personal classroom experience was otherwise. The struggle by Seymour Papert2 to change education to fit the computer, the Turtle geometry debacle aside, was not encouraging. Six millennia of investment in the method of teaching would need more than a philosophical standpoint before it might be transformed. Science was needed. But before science comes a philosophical question. For me it was elegantly expressed by Martin Heidegger3 in “The Question Concerning Technology:” Just what is the essence of technology and how is it that only the modern human has this capacity?
Chapter 1: The Evolution of Technicity
A simple visual comparison of the world half a million years ago, an instant in the long story of evolution, with today’s planet would reveal the appearance of forms that are entirely unnatural. The species that is responsible for this unnatural outbursting is Homo sapiens: yourselves. This chapter is about how you, alone amongst animals, are able to imagine the naturally impossible.
Drawing
I had two children whose drawing skills particularly puzzled me. One was autistic, with a fascinating language deficit, and could draw a frontal view of a bus accurately to scale (except for the writing on the destination board) at the age of four. The other was medically diagnosed as clumsy child syndrome and found it impossible to copy a two column three row grid from a textbook to his exercise book: it came out as three columns and two rows. Nothing in perception could explain this, although perceptual problems were diagnosed by the psychologist. As a teacher, you don’t worry about the diagnosis: you just find a work-around, and I did. But inability to explain is like an itch that won’t go away. So, how do humans draw? The answer is: We have no idea. How we come to be able to make all the illustrations in Richard Gregory’s “Eye and Brain”4 is a closed book. How humans can be geometers and so gain admission to the Academy is a secret: Yet we do it, and devise the Turing machine and go to the moon.
It is not possible for chimpanzees and bonobos to draw. However, Kanzi5, a bonobo, picked up a language based on visual “lexigrams” whilst watching his mother trying to learn this system. In the wild, chimpanzees and bonobos have complex social lives that echo human society. In common with other primates, they cement alliances by social grooming and communicate vocally. Like Kanzi, some members of some troupes make tools and learn by observation6. Evidence available from the fossils of hominines that preceded us and the material associated with them suggests that such behaviour grew in sophistication with increase in brain size. But attempts to train a chimpanzee, which had the rudiments of language, to draw a line dot-to-dot produced inconsistent results7. There is no evidence of any ability to draw before our species appeared. Neither is there evidence that technology, as defined in the OED, had any existence before us8: no other species sought to battle a climate change it had induced.
Speech
Communication, speech (language is too imprecise a word), existed before we did. We can be sure of this for a number of reasons. The first, shown by chimpanzees and bonobos, is that communication using words and grammar can exist without the physical adaptations of speech. Therefore it is safe to say that the will to express what is in mind, as Lois Bloom9 put it, preceded the biological adaptation of a vocal tract. And, as deaf signers know well, speech is not the only medium for expressing to others what is in mind. It is, however, the most efficient and effective in that it frees up the visual channel for other information. It follows that the possession of a fully developed vocal tract implies the possession of a fully developed language10. A fully developed vocal tract would have been present in the common ancestor we share with the Neanderthals because we both inherited it. We also had a brain of similar capacity. In particular, the prefrontal cortex of these species, and I include us, was of a very similar size. As prefrontal cortex, the executive memory of the brain, is responsible for depth and complexity of thought11, it is most likely that they had the same capacity to have things in mind as we have.
Do it like that
What we have in mind that we want to communicate are thoughts about things not obvious from the context. This is shown in the early language development of infants. It is also the information that it is necessary to transmit within a reciprocally altruistic community. Communal planning revolves around memories: past events, the current situation and future prospects. Once Steven Pinker’s12 analysis of language evolution became accepted, there was a flurry of research into possible mechanisms. Robin Dunbar proposed a social13 route to language, linked to intentionality14. His argument is compellingly supported by the everyday uses we make of speech. Daniel Nettle15 nicely fitted language diversity to the prerequisites for reciprocal altruism16 to be in an evolutionary stable state17; and to the family-clan tribal organisation typical of human societies that Hamilton’s rule18 predicts. Given the advantages of the reciprocally altruistic life-style, language characterised by features that identify individuals and thereby their trustworthiness: accents, shifting sound systems, prosody, linguistic diversity, etc. is beautifully crafted to the purpose. There is, however, a problem. It is not possible to plot a path from language to technology. Attempts have been made to derive culture19 from the social-speech complex, but none are convincing. Levels of technological development are as diverse as languages20 yet all languages are equally powerful. Many workers have noted that matters technical are little discussed21,22; and tool use is demonstrated, followed by the words23, “Do it like that.” Here is something “in mind” that cannot be expressed in words. Terrence Deacon24 proposed the co-evolution of brain and speech, which he argued made us the “symbolic species;” but his notion applies equally to Neanderthals. Evolutionary psychology25,26 social/language theories also take us as far as that species but not onward to ourselves.
Deep information
This gap in thinking can be illustrated at an information processing level. It will be useful if we are aware that ‘information’ has rather more to it that the everyday usage suggests. I use the term in the sense denoted by OED sense 3d, where information is equated with entropy. This sense has its origins in James Clerk Maxwell’s demon27, Erwin Schrödinger’s negative entropy28, Claude Shannon’s mathematical definition of information29, Léon Brillouin’s musings about scientific information and physical entropy30 and Tom Stonier’s notion that information defines the internal structure of the universe31. It is not an easy concept. It famously tripped up Stephen Hawking over black holes32. A statistical physical quantity, related to complexity, it has steadily increased since the Big Bang. Life is unusual in that only certain very specific arrangements of matter define a viable organism; as only certain numbers describe a functioning Turing machine33. Ashby’s principle of requisite variety34, the notion than only information can destroy information, is useful when thinking about Darwinian processes. Information/entropy was used in this way by John Maynard Smith and Eörs Szathmáry to describe the major transitions in the evolution of life35.
Transitions are universal: the history of the universe is told through them. They have a very particular property: From the preceding phase before a transition it is impossible to predict the behaviour of the succeeding phase: from the properties of ice you cannot derive the properties of water; from the properties of a prokaryote you cannot predict the properties of a eukaryote. We may apply this test to Maynard Smith and Szathmáry’s alleged final transition: to language. All mammals communicate. And dog, cat or rat owner will attest to their pet’s ability to communicate what they have in mind. Language, in the human sense, is merely more fully developed and represents, in information terms, a shift from individual brains thinking individually to a network of brains sharing what they have in mind. This may be likened to a single computer compared to a network of distributively processing computers: complex problems can be solved more quickly but the capability of the network is no different from that of the individual computer. Maynard Smith and Szathmáry’s analysis, like the social hypothesis, takes us as far as the Neanderthals but no further. We need a transition event that brings in its train totally unpredictable consequences.
The tool illusion
The progress towards modern humans36,37 has been measured by tool assemblages as well as brain size: the bigger the brain the more versatile the tool-kit. But tools are a problematical index. Tools made and used by chimpanzees are ephemeral and the archaeological record knows only stone tools. But stone tools pose questions of their own. A notable issue is stasis: the toolkit associated with Homo erectus changed little for over a million years. Our technology changes daily. So, was the bifacial hande-axe characteristic of this species a tool as we know them or was it genetically inbuilt, like the template for a bird’s nest: what Dawkins38 called an animal artefact, an extension of the phenotype by its genotype? Later, Neanderthals and co-existing anatomically modern humans shared a toolkit that also changed very little. Innovation is the sign we use for modern human behaviour. Sally McBrearty39.40 insists that this was gradual and extends back in time past the point, around 150,000 years ago, that genetics suggests for our speciation event. Tools as such are also inadequate as an index.
Through the classroom window
We can take a rather different viewpoint on the problem by looking into the school classroom. Nursery and kindergarten classrooms are full of colourful construction materials, mark-making equipment, and musical instruments. Infants post shapes through holes in boxes; they nest cups and build towers of blocks; and all in the primary colours: red/green blue/yellow and black and white. This as about as far from the natural world as it is possible to get: nowhere in nature are there carefully graded cups, blocks that are a perfect cube, or solid primary colours. They learn their colours, shapes, and numbers. The children, and those who teach them, seem unperturbed by the fact that they working with natural impossibilities; they even put faces on them.
Children enter primary school with a virtually complete language system but they are at the beginning of their drawing development41,42. This continues apace until they are about ten, thereafter in a more considered way. Their drawings bear no relationship to what they see (realistic representation is a later development for, some). They produce graphical entities that are best described as geometric. Below, fig.1, is a drawing by a four year old43. It may be intended to be a person, but in reality it is a circle, dots, and horizontal and vertical lines. This is not art. It is a construction. It is more engineering drawing than representation. It delineates, describes, key components from the child’s perspective. And that perspective is unreal: chimneys at right-angles to the roof; lines for water level at ninety degrees to the side of a tilted glass, in defiance of gravity.
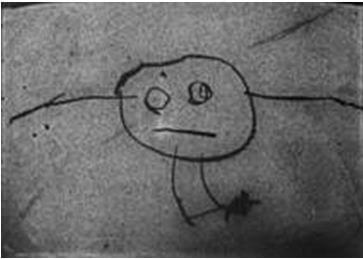 Figure 1, Picture 94532 from the Rhoda Kellogg Child Art Collection
Figure 1, Picture 94532 from the Rhoda Kellogg Child Art Collection
From whence came the information on line, angle, colour, movement and pitch that is so exercised in early years settings? From whence came the lines that are combined to make the letters that they will next learn? From whence came the information on the primary colours they paint with, on paper or a computer screen? Whence the notes on the recorder or xylophone? And from whence the movements that are choreographed into playground games? Seymour Papert44, when attempting to teach turtle graphics “Turtle Talk” as prelude to computer programming, had children “Walk Turtle” in the playground; asserting that they would learn mathematics through “body syntonicity,” i.e. proprioceptively. This idea is of interest because proprioception is phyletic information from the body about the body, not sensory information in the usual sense. However it is not an explanation because there is still no source for the concept of a line for the Turtle to draw. It also misses out an aspect of the feverish childhood drawing phase: its affect. Drawings give pleasure and children enjoy drawing, colouring, constructing, singing, and hopscotch.
Phyletic information
Martin Heidegger, in his almost poetical question concerning technology (from where I take the term technicity) was adamant that the essence (Wessen) of the technology that enframes (Gesell) us will be found to be nothing technological. My suggestion for the source of all this childhood activity, and for the human capacity for technology, is a rather different class of phyletic information. I propose that prefrontal cortex has direct access to the phyletic information immanent in the structure of the primary sensory feature detection neurones45 first described by David Hubel and Torsten Wiesel. They include: line angle and length; direction of motion; the primary colour pairs red/green, yellow/blue, black/white; and pitch. This information is of an entirely different quality to the associated sense data stored in memory. It is elemental and abstract, devoid of meaning. Although line, colour, pitch and motion are present in the environment, they are embedded. The information in primary sensory cortex is a construct of the brain itself, a part of the sensory processing stream. A function of the neural clockwork, it is divorced from sensation: it is unreal in a very deep sense. And it matches very precisely the materiel that is found in the primary school classroom.
Affect and prefrontal access
Shape and colour are loaded with affect. Child drawing is seen as art46 rather than the precursor of ascetic geometry, engineering, writing and arithmetic. It is possible for a colourist to conceive a perfect blue and then seek to create it, with intense joy when success is achieved47. This affective appreciation dimension of colour, shape and sound is highly suggestive of undiluted access by prefrontal cortex, because prefrontal cortex is where limbic and neocortical information meets. That we can construct using these elemental features also indicates prefrontal processing. Once constructed, these unnatural (godless as Friedensreich Regentag Dunkelbunt Hundertwasser48 put it) creations can be stored in memory as if they were the result of normal sensation. Thus, we can have the concept of an ideal square, pure red, and perfect pitch. Once constructed in mind, we can feed the information on the constructive process to pre-motor cortex for assembly into action memory and onward to a manual approximate representation of the ideal (whence straightedge and compass). And, with the concept of a pure red in mind, we can seek out materials from which it might be extracted49. Academic psychologists can use these elements to explore our visual perception by constructing the delightful illustrations we see in works like Gregory’s “Eye and Brain”. I have my own such illustration, fig.2, below:
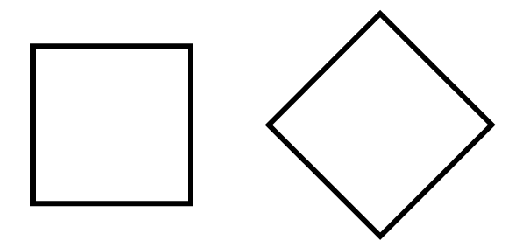 Figure 2. The Shape that Changes its Name
Figure 2. The Shape that Changes its Name
I call it “The Shape that Changes its Name” and it enables us to explore our cognition. If a square is rotated by a one-eighth turn, as from the left to the right figure above, the word “diamond” (unthinkable with the left hand figure) suddenly comes to mind. In other words, we conceive a different object. This is correct in terms of primary sensory processing. The angle detector neurons do not react at all after a 90 degree turn, which is why horizontal and vertical are so distinct. As the figure revolves the output from these neurons diminishes and that from forty-five degree detectors increases. At the mid point the influence from the two is equal but thereafter the diagonal neurons increase in influence until they dominate: a different shape is then perceived. Because the two orientations are neurologically completely different, the language system gives them separate names. Considerable intellectual effort is needed to think of them as the same shape, merely rotated, (as maths teachers will attest).
Another illustration is the Stroop effect. If colours are printed in contradictory words then it becomes difficult correctly to report the colour: green, green. The word ‘green’ makes it more difficult to say “red” for the second colour.
That we are able to counter this conflict is indicative of prefrontal activity. Indeed, the Stroop effect has been used to test prefrontal performance. That language overpowers pure shape and colour supports my contention that the technicity adaptation occurred after language had become established: the error occurs because language lacks a link to colour and shape concepts. Or, rather, the link is indirect, via prefrontal cortex. This is why children in kindergarten and primary school have to ‘learn’ their colours and shapes.
The perverse primacy of language
The relationship between language and the constructions we make from phyletic information is poor. The two processes appear to be independent, only meeting in higher level cognition. In common with emotions, language is a poor medium for communication about constructions: a drawing can convey information about a mechanism in a way that language never can. Conventions of representation tend to be universal whereas language carries its ‘reciprocal altruism’ vs. ‘Machiavellian intelligence50,51’ baggage in train. Disconnection of word and drawing is very deep. We are prone to disregard graphic information where there is competing language. One classic example is Leonardo’s accurate human anatomical drawings. These languished unpublished for three-hundred years whilst Galen’s misleading text retained its place as the surgeon’s bible. The power of language to override higher cognitive processes is very great, and has been much written about in literature52 and guides for social researchers53.
Lithic memory
We do connect the visual with language when we use the elemental graphic forms to represent language in writing. This process removes a significant part of the personal and interfering evolutionary baggage carried in natural speech. It makes the cognitive content that we have in mind, and that we may express in ephemeral speech, into a concrete constructed entity open to public inspection, as Seymour Papert54 put it. But such public entities go beyond writing down words: mechanisms, mathematics and maps are purely visual cognitive products. The ability to make meaningful marks has extended our species’ information capacity by making it possible to store memory externally to the brain. Knowledge may be preserved and passed down generations more efficiently. New learners may use recorded knowledge as a stepping stone to new concepts: the so-called standing on the shoulders of giants. In their turn, they may increment knowledge55. And, because this external memory system can also represent language, we may inspect what we write and use it as a window onto how our mind works, as Steven Pinker has established56. I like to think of this external memory technology as “lithic,” not only because the first writing medium was a clay tablet which dried out and fossilised the writing for all time but also because the term nicely illustrates its nature: writing must be interpreted by a human mind and the information locked within it processed by that mind. Set in stone, only a trained mind may unlock and animate the information to scrawl an answer on a schoolroom slate.
Arithmetic
A nice example of the construction-externalisation-inspection cycle is to be seen in the mathematics of number. It is nice because it appears to take place below the conscious level, as a seemingly subconscious incremental process. Numbers, particularly integers, are unnatural. Most species appear to operate in real number mode, overall quantity rather than precise enumeration57. We humans prefer to nominate rather than enumerate: we name and describe rather than give a number. Few cultures have developed systematic approaches to number: most were agricultural or trading. Only in such societies did the language of number fully develop, and it is notable that even today we attend mainly to the numbers to ten58: the fingers of two hands. When we count things we are prone to error and devise systems to minimize this. Tally systems are common: the five-bar-gate tally (llll) is one method, the ten-bead abacus another. Both are ‘finger counting’. Written number representation was initially only used to represent the outcome of a physical computation, as in the Greek and Roman methods which adapted letters of the alphabet. The invention of the Hindu-Arabic place-value numeral technology changed all this. The system of numerals we use today originates in language, not in physical counting. This technology is rooted in the Indo-European language and the writing used to record it. Thus, the concept of zero was extant, not invented: words for nothing were already present in language. Also, when we enumerate, we mentally shift up, as in Archimedes Sand Reckoner59, in accord with accord with the limit set by Miller’s “Magic Number 7±2.”60 We count to nine and collapse the bundle into a decimal unit on the count of ten. Thus, the word “ten” denotes a higher level unit and not a bundle of ten. The Hindu-Arabic place value system represents this. Of course, as in the car odometer, a mark is required to signal that nothing remains at the lower level: zero, in language “nothing”, “nought”, etc. It took time for this little dot of a place-holder to grow to the status of a numeral.
Because we have extracted methods of dealing with large numbers from language, it is possible to misconceive numbers as being of language61. But number language is but a reflection how of the conceptual capacity of our prefrontal constructive capability is constrained. Nevertheless, once the language of number has developed in response to enumeration, it provides a route to concepts; but one that may be interfered with by inept teaching (see below). So, technology has driven the need to develop enumeration; which in turn evokes language that reflects the working of the brain; which technology enables us to write down and inspect; which makes possible a lithic writing technology that reflects the way our brain processes number; which in turn motivates the invention of a technology and the concepts to perform numerical operations externally to the brain: the once lithic memory is now mechanically animated , independently of a mind. We call the result a computer.
An accidental adaptation?
The evidence in support of The Technicity Thesis is telling, if circumstantial. It would be useful to have a model of how it happened that was sound from the viewpoints of evolution, genetics and neurogenesis. Work on brain shape by Emiliano Bruner62 offers a promising starting point. His comparison of Neanderthal and modern human brain endocasts showed two main differences: a front-back shortening and an increase in the parietal area. The shortening he considered to be the result of non-neurological factors associated with changes to the face and skull for other reasons. The parietal volume increase he thought could be due to neurological factors. When Francis Crick and Christof Koch63 looked in primates for evidence of prefrontal to primary sensory connection they found none, although they noted that there is “some psychophysical evidence in humans that supports” the hypothesis that we are aware of primary sensation. The behaviour of genes64,65, the principles of brain evolution66, the neurogenesis of the prefrontal cortex11 and the Darwinian competition of neurones for connection67 support the possibility that such a connection could occur as a result of neurones growing ‘too far’ for the shortened distance, i.e. being misguided to their former distance in the brain of the precursor species. Here they made a successful though erroneous connection to phyletic primary sensory information. The finding that some fifty percent of neurones die through lack of connection in the process of wiring the brain adds plausibility to this idea. That these elementary sensations have both an affective68 and cognitive dimension also argues for prefrontal connection. If we now factor in the information/entropy principle then the likelihood looks more like a high probability. This is because the human brain approaches the maximum viable size. Reciprocally altruistic networking had only increased the species’ effective information processing capacity. The only additional source of information was the phyletic, evolutionary, information that was stored in the structure of the brain itself. But this is information of a different quality from environmental input: just what is needed for a transition.
Speculation
If this accidental adaptation did occur, and although further research is clearly needed the evidence is compelling, then the conclusions reached by evolutionary biologists, neurologists and psychologists bring us as far as our common ancestor with the Neanderthals, and most probably nicely describe the Neanderthal life-style.
If the only change in brain organisation was accidental connection to primary sensory cortex, probably the visual given the associated and possibly consequent increase in parietal processing capacity, then the effect on the organism would initially have been negligible: merely appreciation of colour, line and motion unavailable to conspecifics. This change might have been effectively neutral, although affective appreciation is seen as beneficial by our species. The process of beginning to make adaptive use of this new information source would require considerable time, time for the rest of the brain to begin to process it and time for the ‘accident’ to become genetically fixed. And, given that the nature of primary sensory information, time would be needed to develop the educational and practical strategies needed for the technological design process39. Camilla Power’s psychologically powerful suggestion of the use of red ochre in the context of menstruation rituals49 points to one route.
This leaves us with the interesting question of what the Neanderthals could and could not do. Of one thing we can be sure: there never was a Neanderthal Banksy, the urge to graffiti is uniquely human. (Note that graffiti is gauchely geometric, not a realistic representation.) If my notion about cognitive construction from basic elements that have an affective dimension is correct, then I do not think that Neanderthals could dance, sing, or design. It seems to me that cognitive appreciation of what an abstract movement or sound is is necessary before they can be combined in choreography or composition. The sounds and movements in the natural environment are all embedded in the context, I can think of no neural mechanism, other than the one I propose, for extracting their essence. Put another way, the abstracted information on motion, line, colour and pitch is unavailable elsewhere in the neural processing system.
However, given the volume of the Neanderthal prefrontal cortex, we can be sure that they were excellent planners: as capable as we are in creating “futures from the past” based on sensory experience. The notion that their lives may have had a spiritual dimension is not ruled out. An awareness of self and others, of kinship, hierarchy and leadership, if coupled to the understanding of past and future that is embedded in syntax, might lead to notions of a spirit world: the anthropomorphisation of the natural world, as children draw faces on inanimate objects and the inhabitants of Sumer believed that spirits inhabited their hand-axe69. But they would leave no trace of this because they could neither draw a face nor craft a bronze hand-axe.
With a language capability on a par with that of the modern human, and in all probability a life-style little different from hunter-gatherer tribes (but no gardening or domestication) it may be that we know more about the Neanderthal mind than we might have thought possible. I remarked earlier that psychology in its plurality stops short at technology, and so did the Neanderthals. Is it possible that behavioural science has only described the “Neanderthal inside us”? Workers with a primatology background in may well have done so: Robin Dunbar’s work on language evolution and intentionality come to mind. Did Terrence Deacon only describe the neurological processes leading to Neanderthal language capability: symbolic, in the sense that he uses the word? As Steven Pinker delves into language, the stuff of thought, which species is he really describing? And, did Lev Vigotsky70 when talking about speech, internal speech and social settings describe the Neanderthal? None of these workers considered the qualitatively different information stream that The Technicity Thesis proposes. If this information was the catalyst for an evolutionary transition, it is likely that it is the only difference between the species; all the rest we have in common. And language, however we value it, is no big deal: just distributed information processing
Chapter 2: With Education
The headline statement of The Technicity Thesis includes the words “with education.” I now return to familiar ground. Technology is unevenly distributed around the globe. Some societies progressed; some remained in stasis; a few regressed20. The important thing about technology is that it can progress and has progressed. This entails not only learning what the older generation knows but adding to that knowledge. The result, for our species, is that little by little we moved from an awareness of line to the ability to draw with Turtle graphics on a computer screen. It follows that the more technology enframes a culture, the more it sets the context for education. Therefore, I will look at teaching methods and media in the well developed English education system before I go on to consider the primary school child and his or her education.
Three methods and media for learning
I want now carefully to define three modes of learning: verbal/demonstrative, lithic and Turing. For this I will use the information/entropy model where, as with energy, information comes in varying degrees of quality. Following this, I will develop the argument for the urgent necessity of a transition of teaching to the Turing medium.
Mode 1. The verbal/demonstrative mode relies on a good memory and the capacity to observe actions and replicate them. The latter has been noted for chimpanzees and, as Robins Burling remarked, is used in human societies to learn tool use and other manual skills. The former is the basis for rote learning. The Neanderthal must have had a good verbal memory and would certainly have been able to learn by observation of a demonstration. So, we modern humans have available a pre-modern human mode of learning; one we share with Neanderthals. Let us mischievously call it Neanderthal.
Mode 2. This mode of learning relies on our ability to make and interpret meaningful marks. I use the word ‘lithic’ to denote it because the first recorded systematic use of this technology was the baked clay cuneiform inscribed tablet of Sumer71. These remnants of the earliest known writing systems include copy-books of school pupils72. However, lithic information must extend back to the time when a modern human first made a meaningful mark; and forward to the scratching of pencil on Victorian school slate. Lithic learning is characterised by a dichotomy between the immutability of the inscribed information and the fluidity with which it must be processed mentally. The medium demands mental agility in its use rather than a pure capacity to remember. Incrementing knowledge is facilitated by the possibility of adding to the store rather than starting anew at each generation. Seymour Papert54 was concerned to emphasise that this mode of learning is facilitated by the construction of a public entity, be it a sand castle or theory of the universe, i.e. by writing or building.
Mode 3. The new, as yet little used mode. I call it Turing learning73. Turing learning uses the stored program digital computer, aka the Turing Universal Machine, as its medium. The difference between the lithic and Turing medium is the character of the public entity constructed: the latter is animated74. Turing machines carry out processes once solely the province of the mind. They read, write, and if instructed do arithmetic. We write these instructions. Education has a politico-conceptual difficulty with this: If children use this mechanical contrivance that has literacy and numeracy inbuilt, surely they will fail to learn and understand the basics upon which education is founded? A not unreasonable position; but what informs this view? Certainly not experience in the use of the medium. Might there just be a question of fear of the unknown?
Information quality
The three modes of knowledge transmission differ markedly in quality of information they employ and transmit, and the learning required for their use.
Mode 1 is founded solely on sense data and its processing by prefrontal cortex. It is useful for learning language and its application and observational learning of tool use and construction. Learning in this mode is environment bound and innovation in any meaningful sense is limited by the rate at which genetic adaptation can occur. Its use is in generational transmission of knowledge by a species that has information sharing ability: specifically language. It is a highly conservative mode.
Mode 2 uses the ability to make meaningful marks on lithic media. This capability, unique to the modern human, is founded in phyletic information from within the sense information processing system: the adaptation that made technicity possible. This, in turn makes the development of technology possible. Technicity then makes possible the devising of means for the external storage of memory. This mode requires the generational transmission of the key to the code used to store memories. Ideographic marks such as simple maps need little learning for their use. Where language is stored, written, a considerable degree of learning is needed to unlock meaning. Additionally, because both graphic and literary representations are of the mind, they can offer a window into how the mind works. This mode enables knowledge to be incremented at a higher rate that genetically possible. It is not environment bound because it employs phyletic information. This is information with a different order of quality order. It offers to the extant brain the potential to generate innovation. This mode is a creative mode, limits to which are set only by the capacity of the brain to produce useful work.
Mode 3 is the outcome of the creative potential of mode 2 and its capacity to offer a window on the working of the mind. The route to the Turing medium intertwines two paths75. One, constructional-engineering, provides the physical basis for the medium; the other, mathematical-linguistic, its conceptual foundation. Both are cognitive, but in different, not well connected, realms. The linguistic and mechanical ran on separate paths for millennia. Physical reckoning used representations of ten digits, often beads on a frame. Number notation was simply shorthand for recording the words used. The Hindu notation went a step further, representing the way we construct number words and thereby beginning to embody mental processes. This in turn led to the pascaline, a gear-based adding machine that is familiar as a vehicle odometer. A parallel process, now that numerals were independent of speech, was the mathematization of language. Outcomes include Boolean algebra, Gödel’s proof and Turing Machine. In the realm of engineering, after a false start with Babbage’s analytical engine, the electronic embodiment of Turing’s theoretical machine brought about the now ubiquitous PC. It combines language and engineering: program and electronics. This mode and medium retains the creative potential of the lithic medium but does away with the absolute necessity for a key to unlock the content. It adds the possibility for users to create processes that are executed out of their mind. This is an entirely novel capability for a medium used in education. We are very familiar with the techniques for and use of the external memory that the old medium provided. How we might best make educational use of the new capacity to store and execute operations externally is very uncertain.
Primary school
Robin Alexander76 recently guided a comprehensive analysis of the primary education system in England. It describes in some detail the historical roots of present practice and made suggestions for the future. The Technicity Thesis was not available when he collated data and thinking. Possibly as a consequence, his analysis of what he called “ICT” lacked the depth he gave to traditional aspects of education. Another possible consequence was the absence of any analysis of modes of learning: language was over-emphasised and there was no analysis of the technologies used. Additionally, the historiographic approach with its traditional academic focus on documentation and the subjects studied in school, with a concomitant social-linguistic emphasis, limited species-level considerations. In particular there was no consideration of neurological correlates of child development, specifically prefrontal cortex maturation, mention of ADHD notwithstanding. This made it impossible to develop aims for primary school that are other than culturally biased. A view from neuroscience will not come amiss.
The primary school child
The foundation for the primary phase of school is built in the kindergarten. Or, more appropriately, the seeds of primary education are sown in the kindergarten: learning is the germination and growth of ideas, biologically embodied in the growth of neuronal connections. We see the beginnings of the processes that will bloom in primary school in the scribbling of a three year old. The illustration below, fig.3, tells us much about the growth to come.
 Figure 3. A drawing by a three year old, from Cox.
Figure 3. A drawing by a three year old, from Cox.
Drawn by a three year old boy42, he called these figures “mummy” and “daddy” as he drew them. The child, fully aware that these pictures looked nothing like his mother and father, used speech to convey his intention. He used speech because this channel of communication is well developed at his age. His scribble signals the developmental beginnings of the visual-graphic communication channel, akin to early babbling. But, and I emphasise this, it is extremely unlikely that this germinating graphic seed will grow into the capability to make a realistic representation of his parents. The ensuing shoot is the seedling of the tree of technicity, on which artistic representation is but a branch. The role of primary school is in nurturing the growth of this uniquely human adaptation so that it may bloom in the secondary and tertiary phases of education.
Prefrontal maturation
The neurology of the primary school child is the neurology of the prefrontal cortex in its developmental phase. Joaqím Fuster11 makes clear the importance of the primary school years for prefrontal connective growth and maturity. Of the two divisions of prefrontal cortex, which are highly interconnected one with another, the orbitomedial connects primarily to the limbic system whilst lateral convexity grows connections mainly to neocortex. Thus, orbitomedial prefrontal cortex is affective in nature67 and lateral prefrontal cortex cognitive. Fed from the older parts of the brain, orbitomedial prefrontal cortex is responsible for moderating goal oriented behaviour, for example, motivation, anticipatory set, selective (inhibitory) attention; all essential for learning. The lateral convexity is the executive of the perception-action cycle. Its information comes largely from memory, learned and instinctual, in sensory and motor cortex; to which sources the technicity adaptation adds the phyletic, structural, information of feature detector neurones (and possibly phyletic information from elsewhere).
The majority of prefrontal connectivity and maturation takes place in the primary school years. By their end, orbitomedial prefrontal cortex is mature. Lateral prefrontal connections are also mostly made in this phase of education, the maturation process continuing into the secondary and tertiary phases and beyond.
Learning
Thus, true learning is an organic process of focused growth. The best example I can give comes from my own experience in learning oxyacetylene welding. The only instruction my teacher could give was, “Move the tip of the flame in a figure of eight and feed in the filler rod.” Presented with a cut-off of sheet steel, I approached the flaring welding torch to it. All I saw through green glass goggles was a searing white light, immediately followed by a hole in the sheet metal. With practice improvement came. The inhibitory attention system somehow removed the redundant information, revealing to me the tip of the flame and the melting metal beneath. After more work to control the hand that fed in the filler rod, I was able to see a globule of molten metal with its cooler oxide layer floating on the top like a continent on an ocean. Moreover, I could move it about whither I wished with the tip of the flame, which now appeared deep blue with a lighter halo. I could begin to learn the skills of the welder.
Primary imperatives
Children come to school with many instinctive, inbuilt, perceptions and conceptions77. This is the basis for cognitive development. However, cognitive connection cannot be the absolute imperative for the primary phase: it is the affective prefrontal cortex that fully matures in this phase, so there is no second chance in secondary school. Looked at from a species perspective, the cognitive complex that is technicity also comes on line during this phase. If we add to this the absolute necessity to develop the complex of communication skills that underpin the reciprocal altruism essential to maintain an increasingly complex technological culture then we begin to draw a picture of the set of priorities that underpin primary school.
The basic skills of literacy and numeracy will still form the core. The former is a means of bringing speech under more effective cognitive control and the latter exercises emerging technicity. But, constructional skills and building up the capacity for teamwork are also a high priority. All must use speech, the only fully developed tool a child brings to school, as a guiding medium. Lastly, although there is no place in primary education for the “subjects” of the secondary and tertiary curriculum, the foundations of the arts, sciences and humanities need to be laid.
The problem with the present primary regime is that the literacy and numeracy core, Alexander’s “curriculum 1,” dominate and distort. This was an absolute necessity for Victorian primary education, expressed as “3Rs”: reading, (w)riting and ‘rithmetic. Rote and lithic were the only learning modes available, the latter embodied in the school slate and pencil. Now that the personal computer is as ubiquitous as was the slate, the latter may be wiped clean and a fresh start made. We can begin to consider how the transition to the Turing medium might ease learning in the basics whilst offering a more constructional medium for other curriculum areas.
Teaching and learning
The three modes of learning exhibit an evolutionary sequence in information quality: from sensory to phyletic to operational. The transition at each stage entails a reduction in biological involvement: an extension of phenotypic cognition into the environment. Meaningful marks that give insight into thinking led to an unnatural externalising of the mechanism of mind. School has used Neanderthal methods and taught lithic media skills for over six millennia. The Turing medium is but six decades old. It is a major transition. The politically astute will now begin to perceive a problem. Six millennia and more of literacy and numeracy, the absolute necessity of the Victorian 3Rs, are at an end. The conservative reaction of the educational establishment was predictable. It is more than a little demeaning to find that the spelling and computational ability that took you to the top of the class is now a property of the educational medium. (The one area of the school curriculum where Turing learning is quietly developing is in the refuge of design-technology.) So, let us ask the question: Just how good are traditional teaching methods? I dropped hints about the mathematics classroom, above, but I turn first to literacy.
Literacy
The Neanderthal within us privileges speech over writing. Speech-primacy is a natural outcome of its evolutionary depth. This makes the task of determining its relationship to writing difficult. The window technicity opens onto speech offers us illumination. Writing has evolved from pictograph through ideograph to the alphabet78. It is another channel through which to express what is in mind, or what you said or want to say. Because writing is a public entity open to inspection, it provides what Bertolt Brecht called a “Verfremdungseffekt.”79 This allows us to step back from speech and listen to it with our inner ear. For professional linguists, this made it possible to write down, with a phonetic alphabet, all the meaningful sound distinctions of a language. For English this led to the conclusion that there were some forty-plus meaning-making sounds or phonemes. But the alphabet has only 27 characters (including the space).
Given the natural drift of these sounds over time, investigated initially by the brothers Grimm80, spelling becomes increasingly divorced from speech as time passes. Anthea Fraser Gupta remarked in her advice to teachers81 that the spelling of English represents the speech of the fourteenth century. But there is a second source of mismatch: accent and dialect82. When an alphabet is used to represent what can be said (as opposed to an ideograph, like a numeral or sign language, that more closely represents what is in mind), the speech of a particular dialect must be selected for graphic incarceration. Writing will, therefore, only ever represent the speech of a certain local community at a particular moment in time. The drift of speech from spelling is illustrated in the OED, which gives a pronunciation guide based on Received Pronunciation (RP) for British English. Englishes in the world diverge markedly from this arbitrary standard, and yet are mutually comprehensible. Jennifer Jenkins83 has shown that the core phonology for intelligibility is less than the forty-odd phonemes. Her “common core” for English as a lingua franca includes most consonants (‘th’ is not one) and long-short vowel distinctions. In practice the latter may be questioned because Glaswegians pronounce ‘food’ with a short ‘u’ rather than the long ‘oo’ of RP. In other words, intelligibility requires no greater a number of meaningfully different sounds than does the alphabet letters. This suggests that what we have in mind before all the artefacts of natural speech are added in84 is “symbolically” closer to writing than is speech. This helps explain why John Downing’s elegantly researched initial teaching alphabet85 failed in every-day classrooms: the assumption that forty six phonemes required representation was invalid.
We may now consider approaches taken to the teaching of reading and writing. The look-say approach clearly relies on memory and the brain’s ability to extract pattern from its input. Phonic methods have more system built in and attempt to map sounds to letters and letter combinations. Synthetic phonics does seem most effective86,87. However, phonics also leads to a tendency for writers to use quasi-phonetic spelling. This happened in the past before spellings were standardised; the OED lists some of these. Today phonetic spelling is not acceptable. Children’s spelling is corrected and examination candidates have had marks deducted for spelling errors.
Synthetic phonics, as currently promoted by government for use in England, takes RP as its reference dialect. However, RP is difficult to map to spellings, both for the reasons Gupta outlined and because one very particular sound is without a letter.
Problems of spelling are of great practical and social importance. It takes significant effort mentally to map the relationship between technologically standard letter and the sound of one’s local dialect. The current ‘best option’ for this is called “synthetic phonics,” which for English maps letters and letter groups to RP. This means that children need to learn RP as an additional accent, as Chris Jolly publisher of a popular phonics scheme has advocated82. Phonics is a help in beginning reading, cf. the i.t.a. but with consequences for spelling. RP includes the schwa, or neutral vowel, (represented by and upside-down ‘e’). This sound has no letter and is a major source of spelling error.
Attempting to spell phonetically is a recipe for ridicule in our literate society and a source of considerable anxiety for those who have not internalised its complexity. So long as literacy learning is based on the lithic medium, there can be no remedy. Only a shift to Turing teaching can transform the situation, and the lives of the afflicted.
The computer can already provide us with text-to-speech conversion, and vice versa, so early literacy as understood in the past is not now so pressing: the information is otherwise accessible. Similarly, the computer keyboard can overcome the problem of fine motor control that so blights children’s early writing. The dictionary built into the word processor can help children correct spellings in real time. But these possibilities are only prosthetic: they do not go to the root of the spelling problem.
The most elegant technical solution entails a switch in focus from speech to writing and takes into account the lingua franca common core sounds. A model is offered by the mnemonic spelling technique of pronouncing mentally a word as spelled. This can be engineered by stripping out all letter-to-sound rules and ersatz prosody that have been introduced to generate natural sounding speech from text84. The outcome, audiotext (autex) as I called it some years ago, would give children access to an ‘accent’ that better maps sound to spelling. Such a system would, for example, always sound the vowel as printed and never the schwa as pronounced. This would help eliminate the wrong-vowel error that is so common. The sound produced would be very unnatural, rather like a beginning reader’s staccato monotone. This is an indication that audiotext might be rather closer to ‘words in mind’ than is realistic speech. Undoubtedly it conveys to a child just how little of natural speech is recorded in writing. The sound might be made more memorable by applying the art of a composer-poet in place of the Frankenstinean stitching techniques that speech engineers now apply to the dissected cadavers of recorded natural utterances; which, as Paul Taylor admits84, does not improve intelligibility. Composition of abstracted sound to create a system with singability is in sympathy with the phyletic primary sensory information that is the foundation of technicity. It would also make its learning pre-reading in the kindergarten appropriate. A singable product would fit not only the nursery ethos but the language learning capacity of the infant. Such a product would also have the potential benefit of providing an international standard to match internationally standard spelling. There is, of course, no research to prove or otherwise the effectiveness of this proposal: the software does not exist therefore it cannot be evaluated. But, is it not perverse to continue with solely traditional methods when the Turing medium offers a potential for improvement?
Numeracy
When children learn the language of number they learn to understand it. Humans are not parrots. Language, with a little stretch of the imagination, can be thought of as the programming language of the brain. When children learn unnatural number language they internalise the structure of the system. Counting things does not help for number concepts above a handful61. Moreover, the poor connection between linguistic and visual information has let to confusion in the classroom. Mathematicians have advised use of so-called structural aids: abacus, number line, Dienes blocks, hundred square and more. All are based on physically counting into bundles of ten. But language bundles on the count of ten into a conceptually higher level unit, not an aggregate. The trick to easy computation is to understand: a) the consistency of the numeral system; and b) its elegant simplicity. I would like to consider how two of these “aids” confuse. First, the abacus: I will take the classic form with rows of ten beads but the principle applies equally to vertical versions. Think about, or carry out if you have an abacus to hand, adding three to eight. The complex set of back and forth manipulations at the eleventh bead interfere with the mental carry at the tenth. This problem has been recognised in Japanese society. They adopted the Chinese abacus which is five-two based, as in fig.4,
 Figure 4. The Chinese abacus
Figure 4. The Chinese abacus
Up to five is counted on then at the sixth count one of the pair of beads is moved and the five cleared. The Japanese simplified this, first by removing the redundant second bead in the row of two and later, C1930 well after the introduction of arabic numerals, by reducing the five to four.
It is possible to visualise a computation on an abacus, and this imaginary calculation progresses at the speed of thought. But, this mental imagery is completely disjoint from the language of number: a phenomenon that I cannot over-emphasise. Thus, the abacus offers a construction whilst the language offers a window on though. It was the latter that led to the Turing machine and stored program digital computer, not the former: the construction was incongruent. Congruence awaited a new construction.
The hundred square is an awfully good, or bad example, of visual-linguistic misconjunction. Look at it, below fig.5:
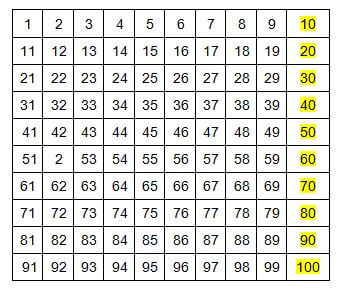 Figure 5. The Hundred Square.
Figure 5. The Hundred Square.
The arabic numerals simply do not fit. The decade numerals should be at the start of the line not at the end. True, if you count the squares you would say words that these numerals are associated with but you do not count with arabic numerals. Arabic numerals are a representational technology with the unique characteristic of matching the working of the mind. This misleading visualisation destroys that relationship. It is a classic, the converse of Leonardo’s anatomical drawing relationship to Galen’s text. Little wonder that children find carrying confusing. Had they been given a calculator there might have been less of a problem, because it works in concert with the mind.
A classroom for construction
The Primary School problem is, however, greater that the use of obsolescent method in literacy and numeracy. As Alexander noted, the aims of primary education are confused and the curriculum confusing. The only mitigating factor is the intuitive understanding of the developing child possessed by certain primary school teachers. What happens in kindergarten and primary school is critical for child development. Good orbitomedial connectivity is essential for all goal oriented behaviour including selective, inhibitory attention; plan execution; anticipatory set and cooperation. The groundings of reciprocal cooperation are established in primary school: an aspect currently relegated to personal, social and health education. It clearly should influence the organisation, method and curriculum of primary school to a significant extent. Children arrive in school with a complete language system, therefore language development in actuality focuses on its use. Skill in discourse is best developed in contexts where a Papertian constructed public entity open to inspection is cooperatively constructed.
If the Turing medium is used for learning, the possibilities for children, and teachers, are significantly increased. More can be done with drawing and writing (in its varied forms) earlier. Colours can be quickly mixed and applied; shapes can be created that are a closer match to the geometric precision that can be imagined; written words can be moved around and their visual appearance changed to produce an attractive result; pictures, words and sound can be combined, and animated. All this is done now. What is missing is the will to do so systematically and thoroughly so that the children gain control of the medium. At present it is fitted in, uninspected, and given low priority.
Such transfer of current learning from lithic to Turing medium does not fully exploit the latter. When the microcomputer first came to school some children actually programmed it, an activity neither they nor their teachers understood. Unfortunately Logo, arguably the most appropriate programming language for children, included the academic conceit of turtle geometry88 with which it became identified. The Turtle, though appealing on the surface, introduces abstractions incompatible with both the curriculum and emerging technicity. Its use therefore declined. Nevertheless, writing for the computer as an audience, i.e. writing a process as opposed to a record, is a necessary extension of writing. A context that proved successful was the control of external objects. LEGO®Logo offered an particularly attractive environment. Partly because of a the crisis in the Lego Company but mainly as a consequence of the failure to teach programming this is now less so. Educational program writing systems regressed to ideograms and so lost the link to natural language. Control of external objects, like turning on a light, can best be expressed by a child in a narrative. Their story can map immediately to computer language, for example “talkto lampa onfor 5”89. It appears perverse, when children are being taught the letters of the alphabet so that they can write what they say, to introduce idiosyncratic and professional-engineering hieroglyphics for programming90,91.
The isolation of modelling and construction from the mainstream primary curriculum is illustrated by the materiel that tends to be used: junk packaging from the weekly shop. But, developing the ability to construct with abstract forms is an essential activity for genesis of technicity. Creating evocative constructions from abstract forms needs to be learned, it does not come easily. The following sequence of forms illustrates just how difficult it is.
 Figure 6. The evolution of the LEGO® Christmas Tree and a classroom original
Figure 6. The evolution of the LEGO® Christmas Tree and a classroom original
It took the Lego Company three attempts over many years before they succeeded in representing the essence of a fir tree, fig.6. The boys in the last picture on the right devised their own abstract representation using ordinary bricks. The LEGO® system is remarkable in its appropriateness for school use; and it is used in many: but not for systematic teaching linked to the core curriculum. It is possible so to do. I know of one example where a systematic approach to working with the computer and LEGO construction is linked directly to and incorporates the normal school curriculum92.
Whither language?
Language is currently asserted to be at the heart of the primary school curriculum but the true purpose of primary school is to nurture technicity development. Development of technicity means learning the skills to construct; be it a LEGO model for inclusion in a cooperative project, a Logo program to animate that project, or the expression of what is in mind in an essay. All of these activities can be undertaken in either a rote or a constructive manner. We can memorise content, rules and their mode of application. We can also develop an understanding of principles, processes and products so that we can combine them creatively. A Neanderthal mind could do only the former, the human mind both. The role of primary education is to assert the uniquely human. This means that language and its use, written and oral, is best developed in contexts that are constructive and cooperative. It means that language-based, verbal, assessment needs to be used with circumspection. A more critical approach to language is required.
Transforming teaching
The transition to Turing teaching should not be unduly difficult. The trick will be first to adapt literacy and numeracy method to the new medium. This should release a significant amount of class time for the important technicity related development in areas such as music, construction, design technology and the graphic arts. The greatest change and challenge is in developing children’s Turing medium capability. Currently this is unsystematically fitted in with little concern for standards of attainment. Children must be taught how to work with computers systematically from the age of entry throughout the primary school years. This cannot be a job for the generalist primary school teacher. There is pressing need for teachers with in-depth appreciation of and capability with the medium. This is not because children will also need to be taught how to “write for the computer as an audience” in computer language; although rhe context in which they are asked to do this will be important: no more mistakes like the great Turtle geometry debacle are needed. Bulgarian experience is useful in this respect because programming was taught without involving Turtle graphics, which at primary level is limited, over abstract and confusing. Rather it is because the process of transfer from “stone age” to Turing teaching entails a major conceptual transition and primary school children are quick to detect and are unforgiving of any lack of facility in their teacher.
There is also the need for time class time and equipment. A minimum of two hours per week from reception to year 6 is required if children are to develop true capability in working with a computer. The Bulgarian “free elective curriculum” devised by Vessela Ilieva has much to commend it, particularly as it has associated software. For teaching, a dedicated computer room is required. In Bulgaria these have a dozen computers for children to work in pairs or individually if the class can be split. Such a room needs a network of serviceable machines, but not the latest offerings. For the medium term, something along the lines of the OLPC laptop for ordinary classroom use is to be preferred. This is not the place to discuss curriculum software design, but it is worth noting that it will solve the literacy and numeracy difficulties I have described, cover normal school subjects and provide information on progress and problems to both teacher and child. It would be reasonable to expect that an eleven plus pupil was a skilled Turing medium user and, hopefully, could touch-type.
Endnote
The Technicity Thesis has now come full circle, reaching the starting point into my concerns that blinkered pre-judgment rather than limited resource was at the root of the educational establishment’s keen assimilation of the computer to extant teaching method and a traditional curriculum. I apologise for straying into realms unthought-of by most teachers of children with learning difficulties. However, I do think that the thesis does attempt to answer questions concerning our evolution as a species more elegantly that those that I have read. I have certainly found the exercise in developing it interesting – a word used to me by a number of academics in a different context. (They couldn’t see a research question.) At a philosophical level, it offers an answer to Martin Heidegger’s question concerning technology. One outcome is the possible need to reclassify our species in the taxonomy. No other species uses phyletic information in the way we do. Technicity is the evolutionary adaptation that catalysed the transition from talking ape to constructive human. As I understand classification systems, this places us in a unique position and we need to recognise it. We may well need a new classification name. (Can we still use “Homo” for both them and us)?
There is final interesting aspect of technicity: the largely low public profile originators of originality. As a friend whose native language is not English put it: “Much clever people work to make the things we have today, nobody knows their names but they do it.” One such is Richard P Gagnon, inventor of the Votrax speech synthesis system. Embodied in the Votrax “Type’Ntalk,” his work sowed the seed of The Technicity Thesis. Such clever people also tend to be given so-called reserved occupations in times of war – an adaptive advantage? Has our species gone beyond the preservation of genes to the preservation of information in a more abstract sense: ideas live on and knowledge increases in depth and complexity: whither Dawkins’ meme?
Summary
- Human beings are the only species to develop technology.
- Language had evolved before the speciation of modern humans.
- In child development the capacity to draw develops after language has fully developed.
- Drawings are constructed from abstract geometrical forms and block-filled with colour.
- Human constructions are unnaturally simple in form.
- The identified source for information on abstract line, colour, etc. is phyletic (elemental) information immanent (inherent) in primary visual cortex.
- Prefrontal cortex has the capacity to create new possibilities from memories.
- Hypothetically, the globularisation of the brain with the advent of anatomically modern humans brought about the accidental connection of prefrontal neurones to primary sensory cortex.
- This would have provided prefrontal cortex with memory information of a different quality from sensory input, thence the technicity adaptation.
- This adaptation is a major transition in life and separates modern humans from all precursor species.
- The unnatural constructions created from this elemental information can only be maintained by a system of education.
- A corollary of the later evolution of technicity relative to language is a disconnection between the two. Technicity and language meet up only in prefrontal cortex.
- Primary education, when prefrontal cortex is making its greatest connectional growth is the phase wherein technicity and language are brought into greater congruence.
- Three modes of learning are available to modern humans:
- Mode 1: pre-modern verbal/demonstrative, which we share with Neanderthals;
- Mode 2: lithic learning, “written on a slate animated in a mind”, uses meaningful marks as external memory, the “Stone Age” basis of schooling since before writing was developed;
- Mode 3: Turing teaching, which uses the computer constructionally, and is new.
- There is evidence to suggest that traditional teaching methods lack conceptual clarity. In literacy and numeracy they confuse children and are unfit for purpose.
- Transition to Turing teaching is the next leap in the development of education. Begun now, a minimum of a quarter century will be required for transition.
To sum up in a short phrase: Technicity enables the human to imagine the naturally impossible.
References and notes
- 1. Doyle, M.P. (1986) Computer as an Educational Medium. MPhil thesis Manchester University
- 2. Papert, S. (1980) Mindstorms. Harvester Press, Brighton.
- 3. Heidegger, M. (1977) The Question Concerning Technology. Harper Torchbooks, New York NY.
- 4. Gregory, R.L. (1966) Eye and Brain. World University Library, London.
- 5. Savage-Rumbaugh, S., & Lewin, R., (1994). Kanzi: The Ape at the Brink of the Human Mind. Wiley, NY
- 6. Matsuzawa, T. Biro, D. Humle, T. Inoue-Nakamura, N. Tonooka, R. and Yamakoshi, G. (2001) Emergence of Culture in Wild Chimpanzees: Education by Master-Apprenticeship.(Pan troglodytes versus). In Primate Origins of Human cognition and Behaviour, T. Matsuzawa (ed.). Springer-Verlag, Tokyo.
- 7. Iversen, I.H. and Matsuzawa, T. (2001) Establishing Line Tracing on a Touch Monitor as a Basic Drawing Skill in Chimpanzees (Pan troglodytes). In Primate Origins of Human Cognition and Behaviour, T. Matsuzawa (ed.). Springer, London.
- 8. Diamond J, (2002) The Rise and Fall of the Third Chimpanzee, Vintage, London
- 9. Bloom, L.: The Transition from Infancy to Language, Cambridge University Press, New York (1993)
- 10. Lewin, R. (1998) Principles of Human Evolution. Blackwell Scientific, Malden MA.
- 11. Fuster, J.M. (2008) The Prefrontal Cortex. Fourth Edition, Academic Press, London.
- 12. Pinker, S. (1995) The Language Instinct. Penguin, London.
- 13. Dunbar, R. (2004) Grooming, Gossip and the Evolution of Language. Faber & Faber, London.
- 14. Dunbar, R. (2004) The Human Story. Faber & Faber, London.
- 15. Nettle, D. (1999) Linguistic Diversity. Oxford University Press, Oxford.
- 16. Trivers, R. (2000) Natural Selection and Social Theory. Oxford University Press, New York.
- 17. Axelrod, R. (2006) The Evolution of Cooperation Revised Edition. Perseus Books Group, New York.
- 18. Hamilton, W.D. (1964) The Genetical Evolution of Social Behavior. Journal of Theoretical Biology 7(1): 1–52
- 19. Dunbar, R., Knight, C. and Power, C. (eds) (1999) The Evolution of Culture, Edinburgh University Press, Edinburgh.
- 20. Diamond, J. (2005) Guns, Germs and Steel. Vintage, London
- 21. Dunbar, R. (1996) The Trouble with Science, New edn., Faber & Faber, London
- 22. Snow, C. P. (1963) The Two Cultures and a Second Look, New English Library, London
- 23. Burling, R. (2007) The Talking Ape, Oxford University Press, Oxford
- 24. Deacon, T.W. (1997) The Symbolic Species. Penguin, London
- 25. Cosmides, L. and Tooby, J. (1992) Cognitive adaptations for social exchange. In The adapted mind (pp. 163–228), J. Barkow, L. Cosmides, and J. Tooby (eds.). Oxford University Press, New York.
- 26. Barrett, L., Dunbar, R. and Lycett, J (2002) Human Evolutionary Psychology, Palgrave, Basingstoke
- 27. Maxwell J. C. (1872) Theory of Heat, 2nd edn,, digitised facsimile online at: http://openlibrary.org/books/OL5682557M/Theory_of_heat.
- 28. Schrödinger E, (1944) What is Life?, online at: http://whatislife.stanford.edu/LoCo_files/What-is-Life.pdf
- 29. Shannon, C.E., & Weaver, W. (1949). The mathematical theory of communication. Urbana: University of Illinois Press
- 30. Brillouin, L. (1956) Science and Information Theory, Academic Press, New York
- 31. Stonier, T. (1990) Information and the Internal Structure of the Universe, Springer-Verlag, London
- 32. Hawking, S. W. (1988) A Brief History of Time, Bantam Press, London
- 33. Penrose, R. (1991) The Emperor’s New Mind, Penguin, London (Now downloadable from various sources.)
- 34. Ashby, W. Ross (1971) An Introduction to Cybernetics. Methuen, London
- 35. Maynard Smith, J. and Szathmáry E. (2000) The Origins of Life, Oxford University Press, Oxford
- 36. Leakey, R. (1994) The Origin of Humankind, Weidenfeld & Nicolson, London
- 37. Stringer, C. and Andrews, P. (2005) The Complete World of Human Evolution. Thames & Hudson, London.
- 38. Dawkins, R. (1999) The Extended Phenotype. Oxford University Press, Oxford.
- 39. McBrearty, S. and Brooks, A.S. (2000) The Revolution that wasn’t. Journal of Human Evolution, 39(5), pp 453-563.
- 40. McBrearty, S. (2007) Down with the Revolution. In Rethinking the Human Revolution, P. Mellors, K. Boyle, O. Bar-Yosef, and C. Stringer (eds.). McDonald Institute Monograph, Cambridge.
- 41. Goodenough, F.L. (1926) Measurement of Intelligence by Drawings. World Book Co, New York
- 42. Cox, M. (1992) Children’s Drawings, Penguin, London
- 43. Rhoda Kellogg Child Art Collection, online at: http://www.early-pictures.ch/kellogg/archive/en/
- 44. Papert, S. (1980) Mindstorms. Harvester Press, Brighton
- 45. Hubel, D.H. (1995) Eye, Brain, and Vision. Online at http://hubel.med.harvard.edu/index.html.
- 46. Gardner, H. (1980) Artful Scribbles. Jill Norman, London
- 47. Ball, P. (2002) Bright Earth: the invention of colour, Penguin, London
- 48. Hundertwasser: http://www.hundertwasser.at/english/texts/philo_verschimmelungsmanifest.p hp
- 49. Power, C. (1999) ‘Beauty magic’: the origins of art, In R. Dunbar, C. Knight, and C. Power, (eds) The Evolution of Culture, Edinburgh University Press, Edinburgh.
- 50. Byrne, R.W. and Whiten, A. (eds) (1988) Machiavellian Intelligence. Oxford Science Publications, Oxford
- 51. Whiten, A. and Byrne, R.W. (eds.) (1997) Machiavellian Intelligence II. Cambridge University Press, Cambridge
- 52. Chang, J. (1991) Wild Swans. Flamingo, London
- 53. Oppenheim, A.N. (1992) Questionnaire Design, Interviewing and Attitude Measurement New Edition. Continuum, London.
- 54. Harel, I. and Papert, S. (1991) Constructionism. Ablex Publishing Corporation, Norwood NJ
- 55. The epistemic process, like all work, is constrained by the second law of thermodynamics
- 56. Pinker, S. (2008) The Stuff of Thought. Penguin Science, London.
- 57. Gallistel, C.R. Gelman, R. and Cordes, S. (2005) The cultural and evolutionary history of real numbers. In Evolution and Culture, S.C. Levinson (ed.), MIT Press, Cambridge, MA.
- 58. For a compendium of language numbers to ten see: http://www.zompist.com/numbers.shtml
- 59. Hawking, S. W. (ed) (2005) God Created the Integers, Penguin, London
- 60. Miller, G.A.: The Magical Number Seven, Plus or Minus Two: Some Limits on our Capacity for Processing Information. Psychological Review, 63, 81-97(1956).
- 61. Elizabet Spaepen, E., Coppola, M., Spelke, E. S., Susan E. Carey, E. S., and Goldin-Meadow, S. (2011) Number without a language model, online at: by Elizabet Spaepen et al. Article #10-15975: 202-334-1310 Proceedings of the National Academy of Sciences (get full ref) PNAS-2011-Spaepen.pdf
- 62. Bruner, E. (2008) Comparing Endocranial Form and Shape Differences in Modern Humans and Neandertals: a Geometric Approach, PaleoAnthropology 2008: 93−106
- 63. Crick, F. and Koch, C. (1995) Are we aware of neural activity in primary visual cortex? Nature 375 121-123.
- 64. Dawkins, R. (1989) The Selfish Gene. Oxford University Press, Oxford.
- 65, Dawkins, R. (1999) The Extended Phenotype. Oxford University Press, Oxford.
- 66. Striedter, G.F. (2005) Principles of Brain Evolution. Sinauer Associates, Sunderland MA.
- 67. Edelman, G. M. (1987) Neural Darwinism, Basic Books, New York
- 68. Damasio, A. (2006) Descartes’ Error: Emotion, reason and the human brain. Vintage, London.
- 69. Kramer, S.N. (1972) Sumerian Mythology Revised Edition. University of Pennsylvania Press, Philadelphia PA.
- 70. Vigotsky, L. (1962) Thought and Language. The MIT Press, Cambridge MA.
- 71. Van De Mieroop, M. (1999) Cuneiform Texts and the Writing of History, Routledg, London
- 72. Kramer, S.N. (1981) History Begins at Sumer: Thirty-nine firsts in man’s recorded history. University of Pennsylvania Press, Philadelphia PA.
- 73. In honour of the homosexual genius whose untimely death, consequent on suppression of his work by government and hounding for his sexual orientation by their agents, denied him the Nobel Prize that he so clearly merited.
- 74. Papert, S. (1994) The Children's Machine. Harvester Wheatsheaf, Hemel Hempstead.
- 75. Augarten, S. (1985) Bit by Bit, Allen & Unwin, London
- 76. Alexander, R. ed. (2010) Children, their World, their Education, Routledge, London
- 77. Bransford, J.D. Brown, A.L. and Cocking, R.R. (eds.) (2000) How People Learn Expanded Edition. National academy Press, Washington DC.
- 78. Robinson, A. (1995) The Story of Writing, Thames and Hudson, London
- 79. This word was used by Bertolt Brecht to describe the so-called alienation effect he attempted in his style of theatre. It implies an ability to stand back from the event and analyse it.
- 80. Grimm’s Rule shows how the Germanic “f” and the Romance “p” in their respective words for fish have the same root sound.
- 81. Gupta, A. F. (2001), Sounds and letters in English, online at: http://www.leeds.ac.uk/english/staff/afg/phonics.html
- 82. Gupta, A. F. (2001) Linguistics at School: Phonics and accents of English, online at: http://www.leeds.ac.uk/english/staff/afg/lagbleeds.html
- 83. Jenkins, J. (2000) The Phonology of English as an International Language, Oxford University Press, Oxford
- 84. Taylor, P. (2008) Text to Speech Synthesis, Cambridge University Press, Cambridge
- 85. Downing, J. (1967) Evaluating the Initial Teaching Alphabet: a Study of the Influence of English Orthography on Learning to Read and Write, Cassell & Company Ltd, London
- 86. Adams, M. J. (1990). Beginning to Read: Thinking and Learning about Print.: The MIT Press. Cambridge, MA
- 87, Rose, J. (2006) Independent review of the teaching of early reading, online at: http://media.education.gov.uk/assets/files/pdf/i/independent%20review.pdf
- 88. Abelson, H. and diSessa A, (1981) Turtle Geometry: The Computer as a Medium for Exploring Mathematics, The MIT Press, Boston, Mass
- 89. LCSI (1995) LEGO Dacta Control Lab Software, Lego Company, Billund
- 90. Scratch: http://scratch.mit.edu/
- 91. LabView, adopted by the Lego Company; http://www.ni.com/labview/whatis/
- 92. Ilieva, V. (2010) LEGO and LOGO in the primary school – a simple way for learning through creation, In: Clayson, E.J., Kalaš, I, (eds) Proceedings of Constructionism 2010 – 12th European Logo Conference. Faculty of Mathematics, Physics and Informatics Comenius University, Bratislava